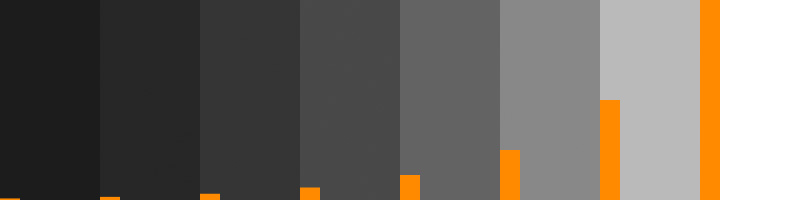It's like a children's book title for the digital cinema crowd: Everybody Clips. The message: It's OK to clip, young digital cinema camera — everyone has to sooner or later. Even film.
It's true. Throw enough light at a piece of color negative and eventually it stops being able to generate any more density. Clipping, i.e. exceeding the upper limits of a medium's ability to record light, happens with all image capture systems.
Everybody clips. So the thing worth talking about is how, and when.
One of the reasons this subject gets confusing is that it starts with understanding a common topic here on Prolost, that of light's linearity and how that linearity is remapped for our viewing pleasure. We all know that increasing light by one stop is the same thing as doubling the amount of light. Yet something one stop brighter doesn't look "twice as bright" to our eyes. We perceive light non-linearly.
Linear-light images, or images where the pixel values are mapped 1:1 to light intensity values, are useful for some tasks (like visual effects compositing) but inconvenient for others. They don't "look correct" on our non-linear displays. And they are inefficient when encoded into a finite number of bits. It's worth understanding that inefficiency, since every digital cinema image (and digital photograph) starts as a linear-light record.
Let's say you have a grayscale chip chart that looks like this:
Each swatch in the chart is twice as reflective as the previous, and photographs as one stop brighter. Each of these swatches is double the brightness of the previous swatch. If you chart those light values, it looks like this:
Each chip is twice as bright as the previous, so each bar is half as high as the next. This image shows off the disparity between measured light and perceived light. Does the swatch on the far right look 125 times brighter than the one on the far left? No, and yet it is.
Notice also how the orange bars representing the reflectance of the swatches are quite short at the left. This is the problem with storing linear light images—they require a lot of fidelity in the shadow areas. One of the many reasons to gamma-encode an image is to better distribute the image brightness values across the available range of pixel values. Here are those same chips, graphed with the gamma 2.2 encoding used to display them:
Note that we now have much more room for variation in dark tones. If we have a limited bid-depth available for storing this image, we're far less likely to see banding or noise in the shadows with this arrangement.
Why is this important? As we've already discussed, it is underexposure tolerance that limits our ability to capture a scene on a digital sensor. We can set our exposure to capture whatever highlight detail we want, but at some point our shadows will become too noisy or quantized to be usable. And this danger is exponentially more apparent when you realize that the chip is capturing linear light values. The first thing we do with those values is brighten them up for display and/or storage, revealing in the process any nastiness in the lower registers.
You can think of the orange bars in the first graph as pixel values. When you shoot the chart with your digital camera, you're using half of your sensor's dynamic range to capture the values between the rightmost chip and the one next to it! By the time you start looking at the mid-gray levels (the center two chips), you're already into the bottom 1/8th of your sensor's light-capturing power. You're putting precious things like skin tones at the weakest portion of the chip's response and saving huge amounts of resolution for highlights that we have trouble resolving with our naked eyes.
This is the damning state of digital image capture. We are pushing these CCD and CMOS chips to their limits just to capture a normal image. Because in those lower registers of the digital image sensor lurk noise, static-pattern artifacting, and discoloration. If you've every tried to salvage an underexposed shot, you've seen these artifacts. We flirt with them every time we open the shutter.
Any amount of additional exposure we can add at the time of capture creates a drastic reduction in these artifacts. This is the "expose to the right" philosophy: capture as bright an image as you dare, and make it darker in processing if you like. You'll take whatever artifacts were there and crush them into nice, silky blacks. This works perfectly—until you clip.
The amount of noise and static-pattern nastiness you can handle is a subjective thing, but clipping is not. You can debate about whether an underexposed image is salvageable or not, but no such argument can be had about overexposure. Clipping is clipping, and while software such as Lightroom and Aperture feature clever ways of milking every last bit of captured highlight detail out of a raw file, they too eventually hit a brick wall.
And that's OK. While HDR enthusiasts might disagree, artful overexposure is as much a part of photography and cinematography as anything else. Everybody clips, even film, and some great films such as Road to Perdition, Million Dollar Baby and 2001: A Space Odyssey would be crippled without their consciously overexposed whites.
The difference, of course, is how film clips, and when.
How does film clip? The answer is gracefully. Where digital sensors slam into a brick wall, film tapers off gradually.
When does film clip? The answer is long, long after even the best digital camera sensors has given up.
More on that in part 2. For now, more swatches! A digital camera sensor converts linear light to linear numbers. Further processing is required to create a viewable image. Film, on the other hand, converts linear light to logarithmic densities. Remember how I described the exponential increase in light values as doubling with each stop? If you graph that increase logarithmically, the results look like a straight line. Here are our swatches with their values converted to log:
Notice that the tops of the orange bars are now a straight line. This is no accident, of course. By converting the image to log, we've both maximized the ability of a lower-bit-depth medium to store the image and we've distributed the image values in a manner that simulates our own perception of light. Exponential light increase is now numerically linear, as it is perceptually linear to our eyes.
We've also, in a way, simulated film's response. As I said, film responds logarithmically to light. In other words, it responds to light much the way our eyes do. This sounds nice, and it is. A big reason is that both film and digital sensors have noise in their responses, noise evenly distributed across their sensitivity. Because film's noise is proportional to its logarithmic response, which matches our perception of light, the result is noise that appears evenly distributed throughout the image. Digital sensors have noise evenly distributed across their linear response, which means that when we boost the shadows into alignment (i.e. gamma encode), we boost the noise as well. This results in images with clean highlights and noisy shadows. Another way to think of it is that in a digital photo of our chip chart, each swatch will be twice as noisy as the one to its right! You can see this simulated below, where I've added 3% noise to the (simulated) linear capture space before applying the gamma of 2.2 for display:
On film, each chip would have roughly the same amount of noise. Film is both more accommodating at the top end and more forgiving of underexposure, as it does not have a preponderance of noise lurking in its shadows.
Next time: Some concrete clipping examples from movies and TV, and more about how the top-end response of film can be simulated by a digital camera.